The Mandelbrot set

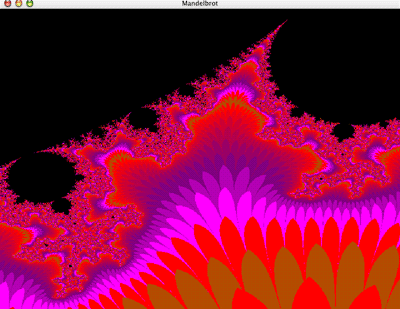
Code for Mandelbrot

//John Lynch Computer Graphics CS 461
// appropriate includes here

#include <GLUT/glut.h>

// function prototypes
void myInit(void);
void myDisplay(void);
//void lineThing(double x1, double x2, double y1, double y2, int level);
//void makeLine(double x1, double x2, double y1, double y2);
void Sp(void);
void Mandelbrot(void);
void drawDot(int x, int y, int color);
int iterate(double x, double y);


//<<<<<<<<<<<<<<< myinit >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
void myInit(void)
{
	glClearColor(1.0, 1.0, 1.0, 0.0) ; // set white background color
	glColor3f(1.0f, 0.0f, 0.5f) ; // set the drawing color
	glPointSize(2.0) ; // a dot is 2 by 2 pixels
	glMatrixMode (GL_PROJECTION) ;
	glLoadIdentity () ;
	gluOrtho2D(0.0, 640.0, 0.0, 480.0) ;
}

//<<<<<<<<<<<<<<< drawDot >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

void drawDot(int x, int y, int color)
{								//draw dot at pixel (x,y)
	glBegin(GL_POINTS);
	
	if (color >= 200)
		glColor3f(0.0, 0.0, 0.0); // if the point is in mandelbrot, color it black (it has a bounded orbit)
	else
		switch( color % 10)			//if the point is not in mandelbrot, color by order of divergence
		{
			case 0: glColor3f(1.0, 0.0, 1.0);	//color by shades of red, yellow, purple
					break;
			case 1: glColor3f(0.7, 0.0, 0.7);
					break;
			case 2: glColor3f(0.5, 0.0, 0.5);
					break;
			case 3: glColor3f(0.6, 0.0, 0.4);
					break;	
			case 4: glColor3f(0.7, 0.0, 0.3);
					break;
			case 5: glColor3f(0.8, 0.0, 0.2);
					break;
			case 6: glColor3f(0.9, 0.0, 0.1);
					break;
			case 7: glColor3f(1.0, 0.0, 0.0);
					break;
			case 8: glColor3f(0.7, 0.3, 0.0);
					break;
			case 9: glColor3f(1.0, 0.0, 0.0);
					break;
		}//end case

		glVertex2i(x,y);
	glEnd();
}


int iterate(double x, double y)
{
	
	/* Iterate each point. If it converges or has a bounded orbit, it will take the count of 200 to knock it out of the loop.
		Color these points black, since they are in the Mandelbrot set.
		If the point "escapes" i.e., goes to infinity, it will happen in less than 200 iterates,
		Color these points by order of divergence - see drawDot*/

	float x1,y1;	
	int count;		 
	int max = 10;
	double cr = x;
	double ci = y;
	x1 = x;
    y1 = y;
	x=0;
	y=0;
	count = 0;
	while((((fabs(x1 - x)) < max) || ((fabs(y1 - y)) < max)) && (count < 200))
	{
		x = x1;
		y = y1;
		x1 = (x*x ) - (y*y) + cr;
		y1 = (2*x*y) + ci;
		count = count + 1;
	}
	return(count);

}





void Mandelbrot(void)
{
	int i,j, color;
	double x,y;
for( i=0; i<=800; i++)				//set the coordinates of each pixel according to the drawing window
	for( j=0; j<=600; j++)
	{
		/* x = -2.0 + (i*3.0)/1280.0;			//window number 1
		 y = -1.5 + (j*3.0)/960.0;*/

		/*x = -1.0 + (i/1280.0);			//window number 2
		y = 0.0 - (j/960.0);*/

		/*x = -1.0 + (i*0.5)/1280;			//window number 3
		y = 0.0 + (j*0.5)/960.0;*/

		/*x = -0.8 + (i*0.1)/1280.0;		//window number 4
		y = 0.0 + (j*0.3)/960.0;*/

		 x = 0.1 + (i * 0.405)/ 1280.0;	//window number 5
		 y = 0.7 - (j * 0.405) / 960.0; 

		/*x = -1.8 + (i * 0.8) / 1280.0;	//window number 6
		y = -.3 + (j *0.6)/ 960.0;*/

		/*x = -1.8 + (i*0.4)/ 1280.0;		//window number 7
		y = -.15 + (j*0.3)/960.0;*/

		/*x = -1.65 + (i*0.4) / 1280.0;		//window number 8
		y = -.15 + (j*0.3)/960.0;*/
		 
		color= iterate(x,y);
		drawDot(i,j,color);

	}
}



//<<<<<<<<<<<<<<< Sp >>>>>>>>>>>>>>>>>>>>>>>>>>>>
void Sp()
{
	glClear(GL_COLOR_BUFFER_BIT); // clear the screen

	Mandelbrot();
	glFlush();		//send all output to display
}





//<<<<<<<<<<<<<< main >>>>>>>>>>>>>>>>>>>>>>>>>>>>
void main(int argc, char** argv)
{

	glutInit(&argc, argv) ; //initializes the toolkit
	glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB) ; //set the display mode
	glutInitWindowSize(800, 600) ; //  setwindow size
	glutInitWindowPosition(0, 0); //set window position on screen
	glutCreateWindow("Mandelbrot"); // open the screen window 
	glutDisplayFunc(Sp) ; // register the redraw functions

	
	myInit(); //additional initializations as necessary
	//glClear(GL_COLOR_BUFFER_BIT) ; //clear the screen
	
	//Sierpinski();
	//lineThing(20, 400, 50, 50, 3);	
	//glBegin(GL_LINES); //use constant GL_LINES here
		//glVertex2i(20, 50);
		//glVertex2i(400, 150);
	//glEnd();

	glutMainLoop() ; // go into a perpetual loop

}